图

图的基本概念

图的定义

无向图。

有向图。

图的术语

完全图。在n个顶点组成的无向图中，若每两个顶点之间都有一条边，则称为无向完全图，它一共有$n(n-1)/2$条边。在n个顶点组成的有向图中，若每两个顶点之间都有方向相反的两条有向边，则称为有向完全图，它有$n(n-1)$条边。

稠密图和稀疏图。如果用n表示图中的顶点数，e表示图中的边数。一般地若$e < nlog_2 n$，则称该图为稀疏图。若$e \geq nlog_2 n$，则称该图为稠密图。

简单路径与简单回路。若路径上各顶点均不互相重复，则称这样的路径为简单路径。若回路中的路径是简单路径，则称为简单回路。简单路径的长度不超过$n-1$。

连通图与连通分量。在无向图中，若从顶点$v_1$到顶点$v_2$有路径，则称顶点$v_1$与顶点$v_2$是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。非连通图的极大连通子图叫做连通分量。

强连通图与强连通分量。在有向图中，若每一对顶点$v_i$和$v_j$之间都存在一条从$v_i$到$v_j$的路径，也存在一条从$v_j$到$v_i$的路径，则称此图为强连通图。非强连通图的极大连通子图叫做强连通分量。

生成树。一个无向连通图的生成树是它的极小连通子图，若图中含有n个顶点，则其生成树有$n-1$条边构成。若是有向图，则可能得到它的由若干有向树组成的森林。

刷题笔记

无向图所有顶点度之和等于边数的两倍。有向图中，出度之和=入度之和=边数。

完全图中，任意两个顶点之间都有直接相连的路径。连通图条件稍弱，两个顶点经过中转结点相连也行。

一个无向完全图有$n(n-1)/2$条边。有向完全图有$n(n-1)$条边。

一个无向连通图的至少有$n-1$条边，若刚好有$n-1$条边即为生成树。

一个有向强连通图至少有n条有向边，此时构成一个大的圆环。

深度优先遍历、拓扑排序可以判断一个有向图是否有回路。

具有n个结点的有向无环图最多有n(n－1)/2条边

可以这样理解当第一个结点指向其他n-1个结点时第二个结点只能指向其余n-2个结点而不能指向第一个否则成环。

可以从拓扑排序角度理解为何最大，假设图用邻接矩阵存储同时编号成三角矩阵(有向无环图可以拓扑排序肯定可以编号)，当存满上(或下)三角矩阵时边达到最多。假设还有有向边在下(或上)三角则必定成环。

图的存储及基本操作

邻接矩阵

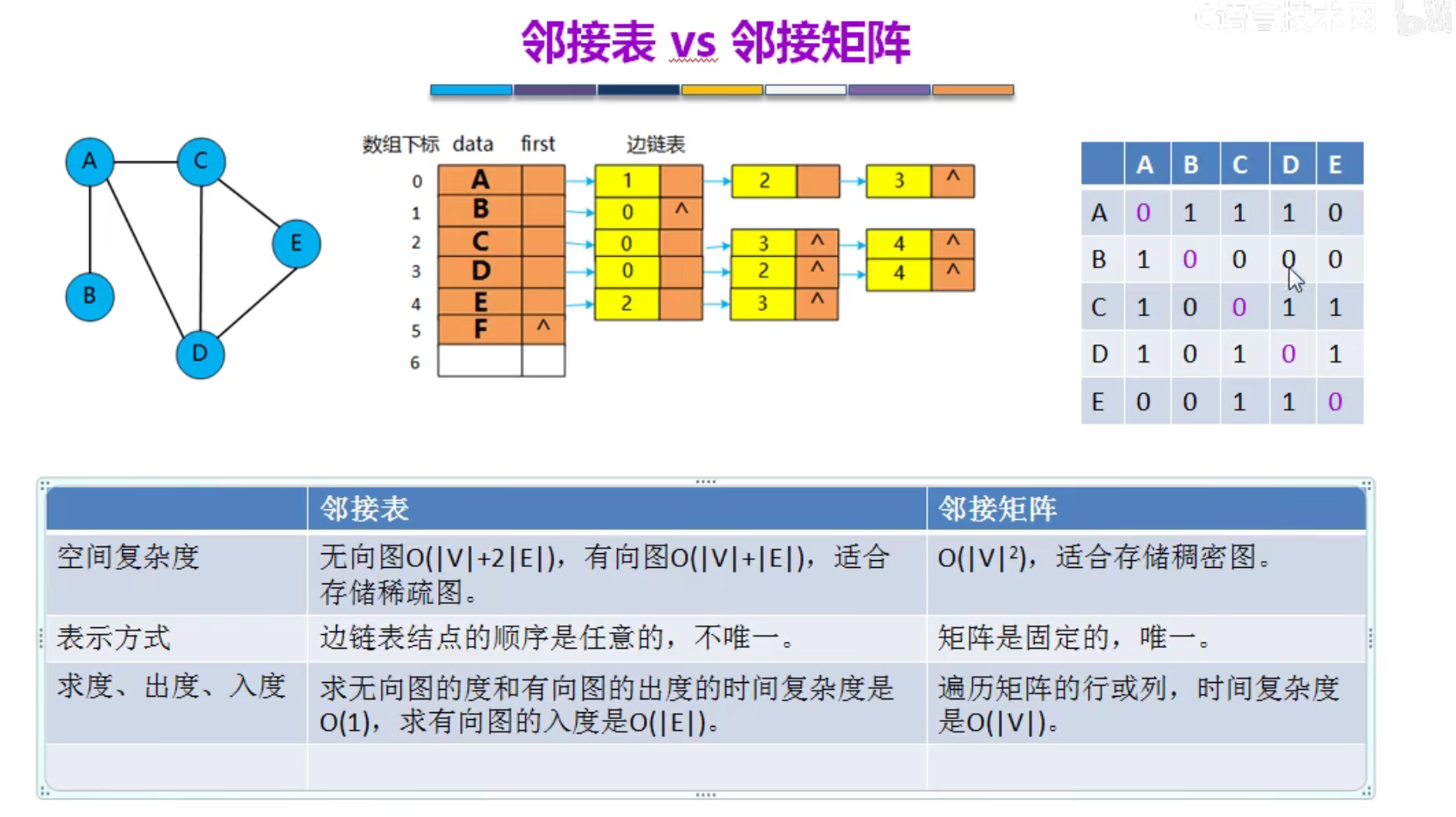
邻接表

十字链表

十字链表是有向图的一种链式存储结构。主要解决有向图求顶点入度和初度困难的问题。相当于将邻接表和逆邻接表结合起来。

邻接多重表

邻接多重表是无向图的另一种存储方式。主要解决无向图每条边都要存储两遍的问题。对无向图而言，其邻接表和邻接多重表的差别仅在于：同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。

图的遍历

图的应用

最小生成树

普里姆（Prim）	克鲁斯卡尔（Kruskal）
从任意顶点开始构建生成树；然后将代价最小的其他顶点纳入生成树，直到所有的顶点都纳入为止。	每次选择一条权值最小的边，让这两条边两端顶点连通，连通之后不能构成回路，否则不选。
适用于稠密图（边多）	适用于稀疏图（变少）
时间复杂度$O(	v

Prim算法每次从所有已经确定的顶点发出的边中，选择权值最小的且不会构成回路，解决的是最小生成树问题。

Dijkstra算法每次只从源点的所有可到达的顶点（直接或间接）中选择代价最小的，解决的是单源最短路径问题。

最短路径

Dijkstra

对图G(V,E)设置集合S，存放已被访问的顶点，然后每次从集合V-S中选择与起点s的距离最小的一个顶点（记为u），访问并加入集合S。之后，令顶点u为中介点，优化起点s与所有从u能到达的顶点v之间的最短距离。这样的操作执行n次（n 为顶点个数），直到集合S已包含所有顶点。

Dijkstra算法不能处理图中权值出现负数的情况。

Floyd

顶点$v_i$经过顶点$v_j$到达$v_k$长度能否变短。

Floyd算法允许有带负权值的边，但不允许有带负权值的边组成的回路。

拓扑排序

设有向图有 n 个顶点 e 条边，进行拓扑排序时总的时间复杂度为 $O(n + e)$

关键路径

在一个表示工程队的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们成之为AOE网（Activity On Edge Network）。

用一个有向图表示一个工程的各子工程及其相互关系，其中以顶点表示活动，弧表示活动之间的优先制约关系，称这种有向图为顶点表示活动的网，简称AOV网（Activity On Vertex network）。

我们把路径上各个活动所持续的时间之和称为路径长度，从原点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动称为关键活动。

两个核心概念：

• 只有在某顶点所代表的事件发生后，从该顶点出发的各个有向边所代表的活动才能开始。
• 只有在进入某顶点的各个有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。

注意：关键路径上的活动称为关键活动，顶点是事件。关键活动没有余量，而不是事件没有余量。

图与表达式

图的存储

邻接表

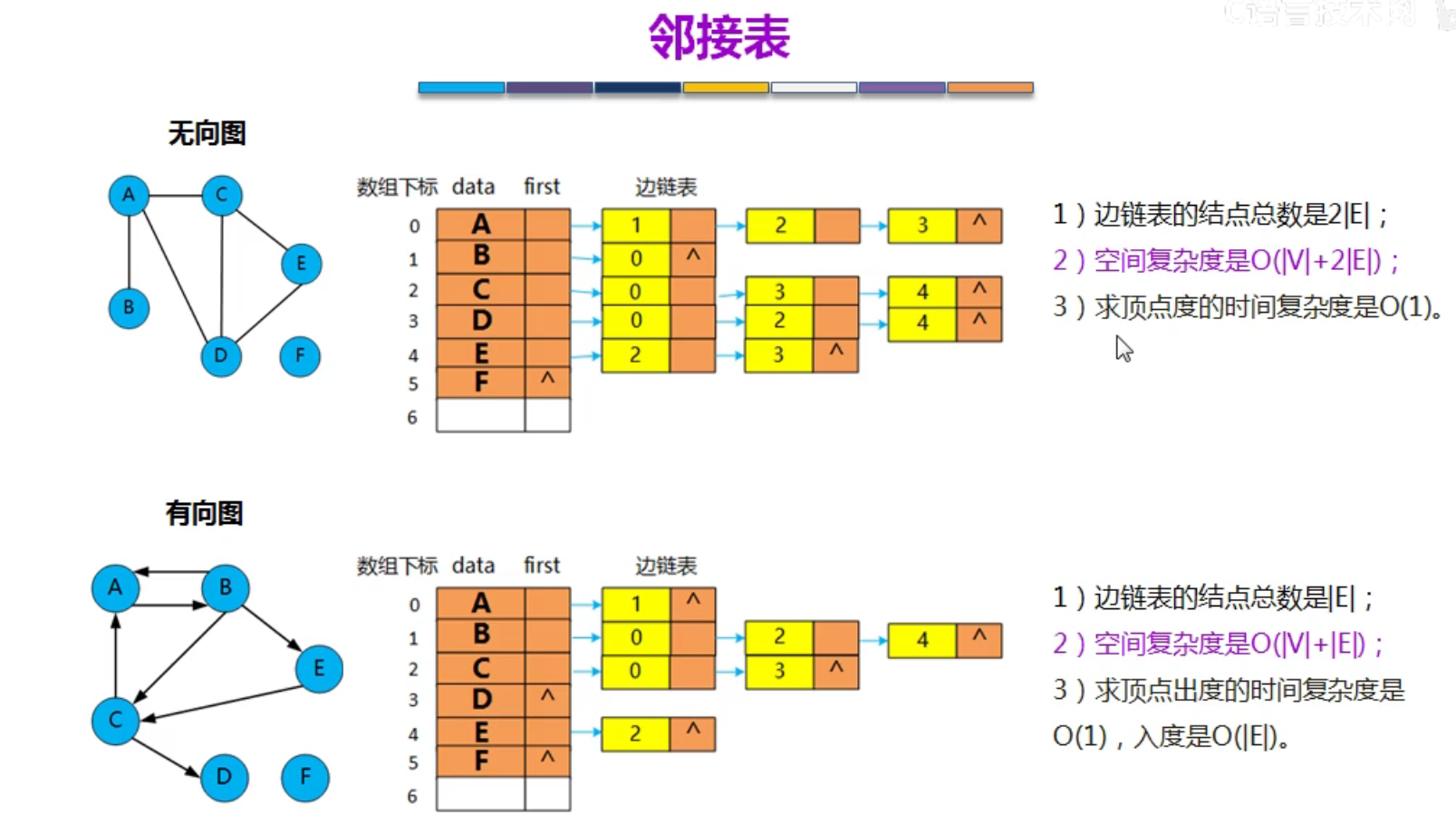
无向图

一个有n个顶点的无向图最多有$n(n-1)/2$ 条边

关键路径