树
二叉树
二叉树的递归定义:
- 要么二叉树没有根结点,是一棵空树
- 要么二叉树由根结点、左子树、右子树组成,且左子树和右子树都是二叉树。
注意区分二叉树与度为2的树
对于树来说,结点的子树是不区分左右顺序的。因此度为2的树只能说明树中每个结点的子结点个数不超过2.
对于二叉树,不仅满足每个结点的子结点个数不超过2,而且左右子树是严格区分的,不能随意交换左右子树位置。
二叉树创建
使用层次遍历创建二叉树比较方便,但是编写代码时需要注意一个问题。
每当申请一个新结点时,它的左右两个孩子指针都是NULL。所以如果只是将子结点的指针入队,入队时的内容就为NULL。那么出队的时候也出NULL,就无法分辨入队的是属于哪个结点的子结点指针。无法形成二叉树。
为了避免这种情况,我们将指向子结点的指针的地址(指向子结点的二级指针)入队,用以辨别这是哪个结点的子结点指针。
比如对于第一个结点,输入了它的两个子结点的的指针的地址。随后出队的时候出的就是指向第一个结点的左子结点的指针的地址,通过<*地址>的取该地址内的内容我们就可以去控制它的左子结点指针指向。
BiNode* newNode(int data) {
BiNode* n = new BiNode;
n->data = data;
// 初始状态下没有左右孩子,也就是该结点的左右指针指向NULL
n->lchild = n->rchild = NULL;
return n;
}
// 根据层次遍历创建二叉树
void init(BiTree& root, int* arr, int len) {
queue<BiNode**> qu; // 注意队列里存的是指针的地址,也就是二级指针
qu.push(&root);
for (int i = 0; i < len; ++i) {
BiNode** n = qu.front(); // 去除一个指针
qu.pop();
if (arr[i] != -1) {
*n = newNode(arr[i]); // 改变指针的指向
qu.push(&(*n)->lchild); // 将左右孩子指针的地址入队
qu.push(&(*n)->rchild);
}
}
}二叉树遍历
如果一个二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足所有的结点全部没有左子树或者所有的结点全部没有右子树,即二叉树的高度等于结点数。
树和二叉树遍历对应关系
| 树 | 二叉树 | 森林 |
|---|---|---|
| 先序遍历 | 先序遍历 | 先序遍历 |
| 后序遍历 | 中序遍历 | 中序遍历 |
树的先序对应二叉树的先序,树的后序对应二叉树的中序。
二叉树层序遍历
递归版本
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
class Solution {
public:
/**
*
* @param root TreeNode类
* @return int整型vector<vector<>>
*/
vector<vector<int> > levelOrder(TreeNode* root) {
// write code here
vector<vector<int>> res;
dfs(res, root, 0); // 采用深度优先遍历的方案
return res;
}
void dfs(vector<vector<int>>& res, TreeNode* root, int level) {
if(root == NULL) return; // 判断根节点是否是NULL,是则返回
if(level >= res.size()) res.push_back({}); // 判断是否需要在res中多填一向量组,因为我们下面要用索引访问
res[level].push_back(root->val); // 用level决定将当前的结点值放置到哪一个索引对应的res的子向量中
dfs(res, root->left, level+1); // 继续递归左子树(左子树必须先递归)
dfs(res, root->right, level+1); // 继续递归右子树
}
};递推版本
class Solution {
public:
/**
*
* @param root TreeNode类
* @return int整型vector<vector<>>
*/
vector<vector<int> > levelOrder(TreeNode* root) {
// write code here
vector<vector<int>> ans;
std::queue<TreeNode*> qu;
qu.push(root);
while(!qu.empty()) { // 如果队列非空
int n = qu.size(); // 获取每一层的结点数
vector<int> tmp;
TreeNode* p;
while(n--) { // 处理n个结点
p = qu.front();
tmp.push_back(p->val);
// 下一层结点入队
if(p->left != nullptr) {
qu.push(p->left);
}
if(p->right != nullptr) {
qu.push(p->right);
}
qu.pop();
}
ans.push_back(tmp);
}
return ans;
}
};完全二叉树
性质
如果对一棵有n个结点的完全二叉树(其深度为$\lceil log_2(n+1) \rceil $ )的结点按层序编号(从第 1 层到第$\lceil log_2(n+1) \rceil $)层,每层从左到右),对任一结点 $i \left( 1\leq i \leq n\right)$ 有:
- 如果 i = 1, 则结点 i 是二叉树的根, 无双亲;如果 i > 1,则其双亲是结点 [i/2]
- 如果 2i > n,则结点 i 无左孩子(结点 i 为 叶子结点);否则其左孩子是结点2i
- 如果2i + 1 > n, 则结点 i 无右孩子;否则其右孩子是结点 2i + 1
- 以上性质只适用于完全二叉树,一半的二叉树没有这些特性。
完全二叉树的最后一个结点的编号是n,则它的父结点,也就是最后一个分支结点的编号为$\lfloor n/2 \rfloor$,则叶子结点个数为n-$\lfloor n/2 \rfloor$。
例如,完全二叉树的最后一个结点的编号是1001,则它的父结点的编号为1001/2=500,则叶子结点个数为1001-500=501.
$$ 度数和=边数=节点数-1 \ 2n_2 + n_1 = n_0 + n_1 + n_2 - 1 \ n_0 = n_2 + 1 $$
非空二叉树上第k层上至多有$2^{k-1}$个结点。
高度为h的二叉树至多有$2^h -1$个结点。
具有n个结点的完全二叉树的高度为$\lceil log_2(n+1) \rceil $
完全二叉树度为1的结点$n_1$只可能取1或0
最胖的树最矮,最瘦的树最高。
遍历
任何一棵二叉树,无论先序、中序还是后序,左孩子一定在右孩子之前。如果两个不同的遍历次序之后,其中两个结点先后次序不一样,则说明这两个结点不是左右兄弟关系。例如当两个结点的前序序列为XY,后序序列为YX时,则X是Y的祖先。
前序遍历时需要借助栈。前序序列和后序序列的关系相当于以前序序列为入栈次序,以中序序列为出栈次序。
中序序列可以与先序序列、后序序列、层序序列中任意一个来构建唯一的二叉树,而后三者两两搭配或是三个一起上均无法构建唯一的二叉树。原因是先序、后序、层序均是提供根结点,作用是相同的,都必须由中序序列来区分左右子树。“先序看最前,后序看最后,中序指示左右子树。”
线索化
利用建立的线索二叉树找某个结点的前驱或者后继,仍不能有效解决先序线索二叉树找先序前驱和后序线索二叉树找后序后继。
先序遍历(中左右)、中序遍历(左中右)的最后访问的结点都是左或右叶结点,叶结点是没有子树的,所以两个指针域空出来了,可以存放线索指针。但是后续遍历(左右中),最后访问的是子树的根结点,而子树根结点的两个指针域都指向子树了,所以不能空出来存放线索信息。
表达式与二叉树
表达式二叉树的先序遍历结果就是先缀表达式。同理,中序遍历是中缀表达式,后序遍历是后缀表达式。
https://zhuanlan.zhihu.com/p/54670963
输出带括号中缀表达式
算法思想:基于二叉树的中序遍历,但是我们要给关键位置加上左括号和右括号。除了根结点和叶子结点,遍历到其他结点的时候,在遍历左子树之前加左括号,遍历完右子树后加上右括号。
二叉排序树(BST)
对二叉排序树进行中序遍历,可以得到一个递增的有序序列。
树转成二叉树
加线:在所有的兄弟结点之间加一条线
去线:对树中每个结点,只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
层次调整:以树的根结点为轴心,将整颗树顺时针旋转一定的角度,使之结构层次分明。比如结点A,保留第一个孩子B,成为左孩子,A的其余孩子均成为B的右孩子。
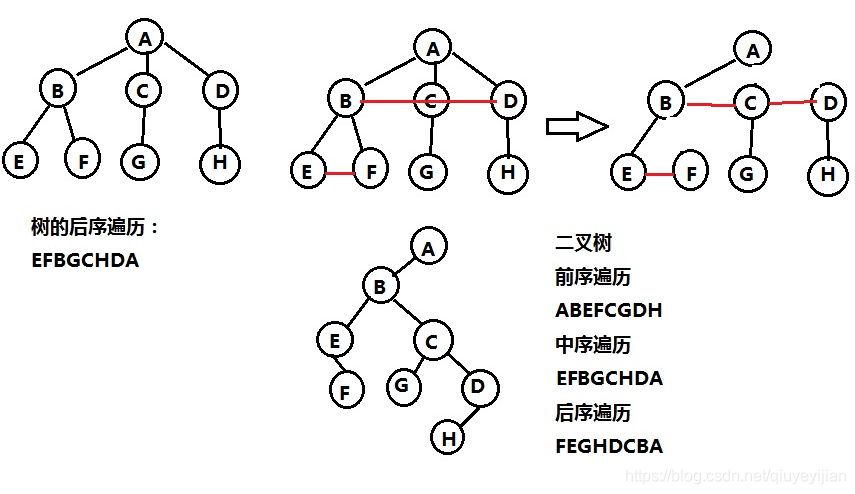
任何一棵和树对应的二叉树,其右子树必定为空
中序遍历时间复杂度
https://blog.csdn.net/qq_43152052/article/details/90111095
代码题
满二叉树前序转后序
void preToPost(char *arr, int begin, int end) {
// 保存根结点数值,留待最后输出,开始位置向后挪动一个位置
// 相当于将先序遍历头结点转变成后序遍历最后结点
char root = arr[begin++];
// 继续划分左右子树,递归
// 因为是满二叉树,中间位置正好是左右子树界限
int mid = (begin + end) / 2;
if (begin <= end) {
preToPost(arr, begin, mid);
preToPost(arr, mid + 1, end);
}
printf(" %c", root);
} 秋叶依剑
秋叶依剑