算法概论
算法的概念
什么是算法
算法的设计应满足以下几个目标:正确性、可使用性、可读性、健壮性、高效率与低存储量需求。
算法应具有以下5个重要特性:有限性、确定性、可行性、输入性、输出性。
算法和数据结构
算法和数据结构既有联系又有区别。
数据结构是算法设计的基础。算法的操作对象是数据结构,在设计算法时通常要构建适合这种算法的数据结构。数据结构的设计主要是选择数据结构的存储方式,例如确定求解问题中的数据采用数组存储还是采用链表存储等。算法设计就是在选定的存储结构上设计一个好的算法。
另外,数据结构关注的是数据的逻辑结构、存储结构以及基本操作,而算法更多的是关注如何在数据结构的基础上解决实际问题。算法是编程思想,数据结构则是这些思想的逻辑基础。
算法分析
通常有两种衡量算法效率的方法:事后统计法和事前分析估算法。前者存在这些缺点:一是必须执行程序,二是存在其他因素掩盖算法本质。所以我们一般采用事前分析估算法来分析算法效率。
数学基础
- 算术级数
$$ \displaystyle \sum^{n}_{k=1}{k} = n (n+1)/2 $$
- 几何级数
$$ \displaystyle \sum^{n}_{k=0}{x^k} = \frac{x^{n+1} - 1}{x-1} $$
- 调和级数
$$ \displaystyle \sum^{n}_{k = 1}{\frac 1 k} = logn $$
- 其他级数 $$ \displaystyle \sum^{n}_{i=1}{i^2} = n (n+1)(2n+1)/6 $$
$$ \displaystyle \sum^{n}_{k=1}{2^{k-1}} = 2^n -1 $$
$$ \displaystyle \sum^{n}_{k=1}{logk} = nlogn $$
主要定理
1、分治法主定理
所谓分治算法是把一个问题划分成多个子问题,每个子问题是原问题的一部分,然后执行一些额外的工作来计算最后的答案。
例如,归并排序算法计算两个子问题,每个子问题都是原问题规模的一半,然后利用O(n)时间的额外工作完成归并。时间公式为: $$ T(n) = 2T(\frac{n}{2}) + O(n) $$
下面的定理可以用来确定分治算法的运行时间。对于一个给定的程序(算法),首先尝试找到问题的递归关系。如果问题的递归满足下面的公式,那么可以直接算出时间复杂度: $$ T(n) = aT(\frac{n}{b}) + O(n^klog^pn) $$ 其中:$a >= 1, b > 1, k >= 0 且 p 是实数$,则:
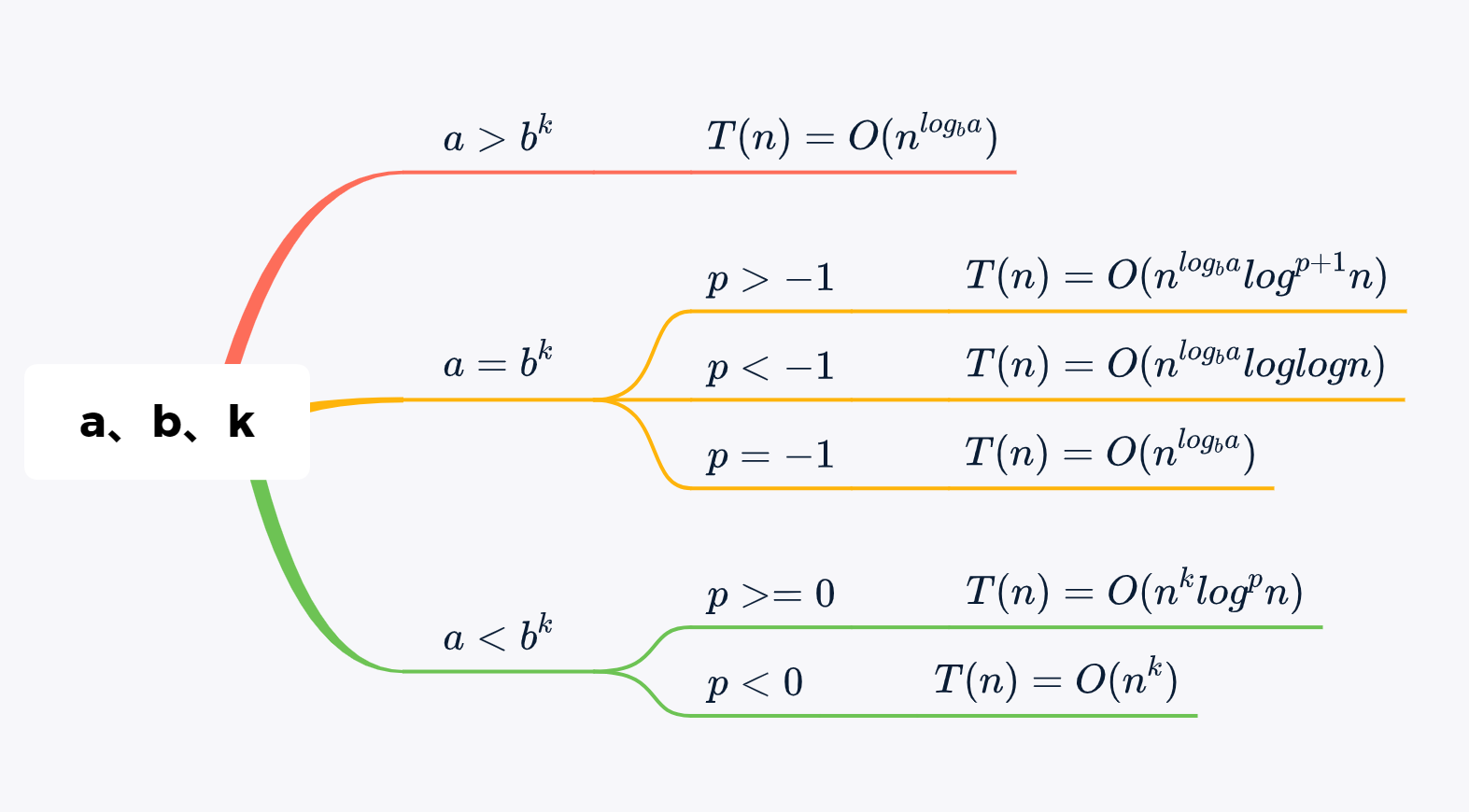
2. 问题规模减小和递归求解主定理
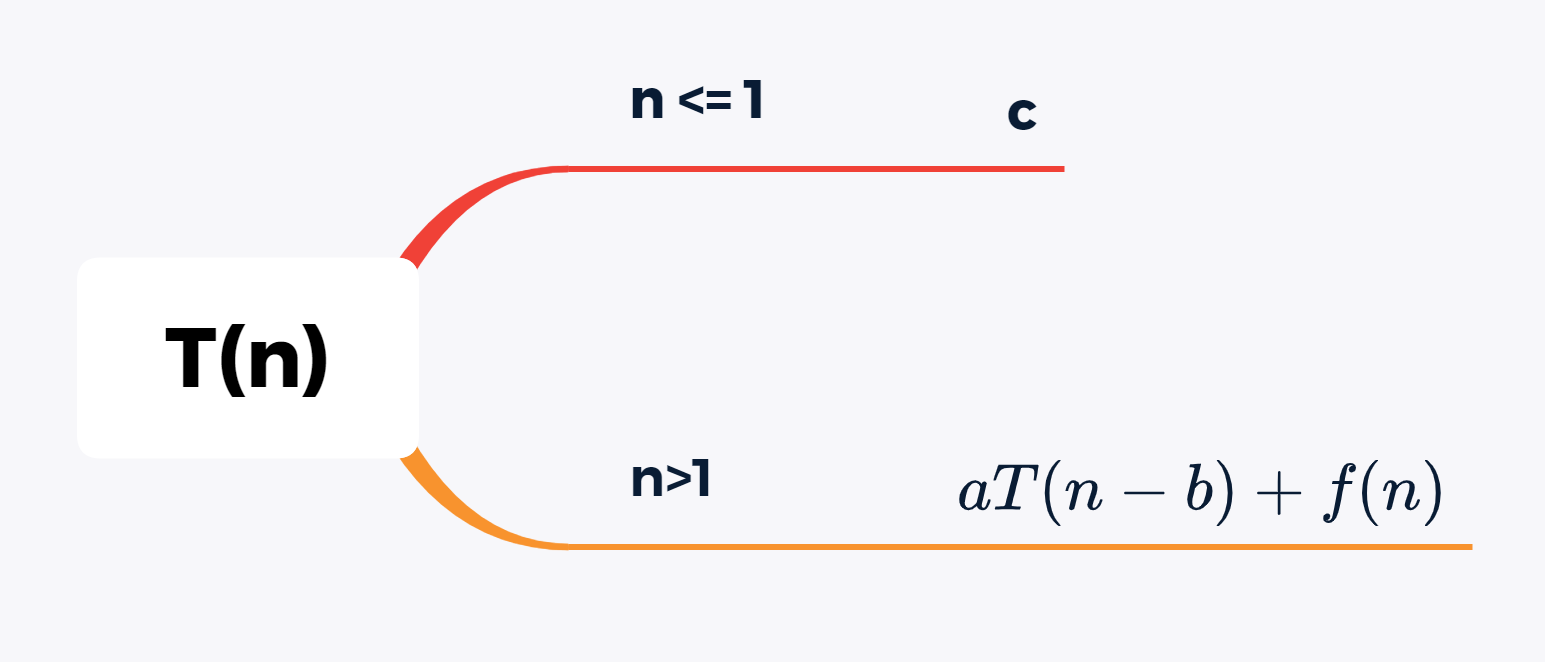
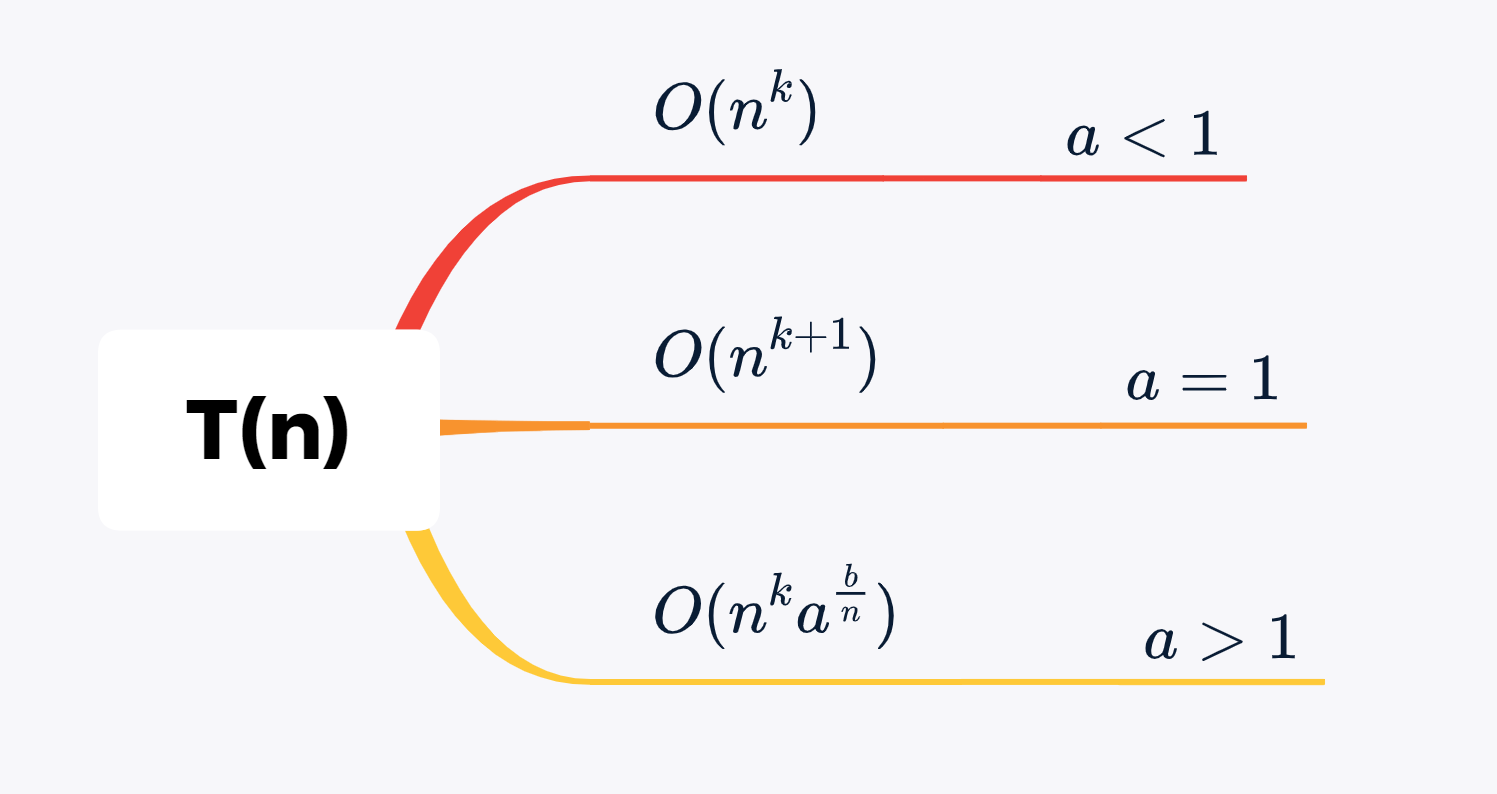
实战演练
第一题
void function(int n) {
int i = 1, s = 1;
// s每次增减i
while(s <= n) {
i++;
s += i;
printf("*");
}
}如果k是函数迭代的总次数,那么当循环终止时应该满足的条件是: $$ 1 + 2 +...+k = \frac{k(k+1)} {2} > n \quad => \ k = O(\sqrt n) $$
第二题
void function(int n) {
int count = 0;
// 外层循环执行 n / 2 次
for(int i = n / 2; i <= n; i++) {
// 中间循环执行 n / 2 次
for(int j = 1; j + n / 2 <= n; j++) {
// 内层循环执行logn次
for(int k = 1; k <= n; k *= 2) {
count++;
}
}
}
}时间复杂度:$O(n^2logn)$
第二题
void function(int n) {
// 常数时间
if(n == 1) return;
// 外层函数执行n次
for(int i = 0; i < n; i++) {
// 由于break语句,内层循环只执行了一次
for(int j = 0; j < n; j++) {
printf("*");
break;
}
}
}时间复杂度:$O(n)$
第三题
void function(int n) {
// 外层循环执行n次
for(int i = 1; i <= n; i++) {
// 里层循环执行 n / i 次, j每次增加i
for(int j = 1; j <= n; j += i) {
printf("*");
}
}
}对于每一个i,内层循环执行n / i 次。运行时间是: $$ n \times (\sum^{n}_{i = 1}{n / i}) = O(nlogn) $$
第四题
void function(int n) {
// 常数时间
if( n == 1) return;
// 外层循环执行n次
for(int i = 0; i < n; i++) {
// 内层循环执行n次
for(int j = 0; j < n; j++) {
// 常数时间
printf("*");
}
}
function(n - 3);
}显然代码的递归表达式为$T(n) = T(n-3) + c \cdot n^2$,其中常数 $c > 0 $。输出语句执行$n^2$次,递归调用自身输入规模是$n-3$。
根据问题规模减小和递归求解主定理,求得$T(n) = O(n^3)$
第五题
void function(int n) {
int k = 1;
while(k < n) {
k *= 3;
}
}循环终止条件是$3^i \geq n$,$i >= log_3n$ 所以时间复杂度为$O(logn)$
第六题
确定如下递归关系的渐进时间复杂度 $$ T(n)\begin{cases} 1 & n = 1 \ T(n-1) + n(n-1) & n \geq 2 \end{cases} $$
此问题可以用分治法主定理公式求解,下面给出迭代分析的过程: $$ T(n) = T(n-2) + (n-1)(n-2) + n(n-1)\ ...\
T(n) = T(1) + \sum_{i=1}^{n}i(i-1) \ T(n) = T(1) + \sum_{i=1}^{n} i^2 - \sum_{i=1}^{n} i \ T(n) = 1 + \frac {n(n+1)(2n+1)} {6} - \frac {n(n+1)} {2} \ T(n) = O(n^3) \ $$
第七题
void function(int n) {
// 外层循环执行n次
for(int i = 0; i < n; i++) {
// 里层循环执行 n / i 次, j每次增加i
for(int j = 0; j < n; j += i) {
printf("*");
}
}
}对于每一个i,内层循环执行n / i 次。运行时间是: $$ n \times (\sum_{i=1}^{n} n / i) = O(nlogn) $$
第八题
void function(int n) {
// 常数时间
if(n <= 1) return;
// 执行三次值为n-1的递归调用
for(int i = 0; i < 3; i++) {
function(n-1)
}
}只考虑三次递归调用。这意味着时间复杂度为:
$$ T(n)= \begin{cases} c & n \leq 1 \ c + 3T(n-1) & n \gt 1 \end{cases} $$
利用问题规模减小和递归求解主定理,可得: $$ T(n) = O(3^n) $$
第九题
void function(int n) {
if(n <= 1) return;
else {
printf("*");
// 递归调用,参数值为2
function(n/2);
// 递归调用,参数值为2
function(n/2);
}
}函数递归公式为: $$ T(n) = 2T(n/2) + 1 $$ 根据主定理: $$ T(n) = O(n) $$
第十题
void function(int n) {
int i = 1;
while(i < n) {
int j = n;
while(j > 0) {
// logn次
j = j / 2;
}
// logn次
i = 2 * i;
}
}时间复杂度为$O(logn * logn) = O(log^2n)$
第十一题
int i = 1, n;
while( i < = n) {
j *= 2
}对于任意$n \gt 0$,循环执行的比较次数为:$ceil(log_2n) + 1$
第十二题
void function(int n) {
// 执行n次
for(int i = 0; i < n; i++) {
// 执行n*n次
for(int j = 0; j < i*i; j++) {
if(j % i == 0) {
// 执行j = n*n次
for(int k = 0; k < j; k++) {
printf("*");
}
}
}
}
}时间复杂度为:$O(n^5)$
第十三题
int fact(int n) {
if(n <= 1) return 1;
return n * fact(n-1);
}
时间复杂度:$O(n)$ 秋叶依剑
秋叶依剑