计算机组成原理
数据的表示和运算
定点数的表示与运算
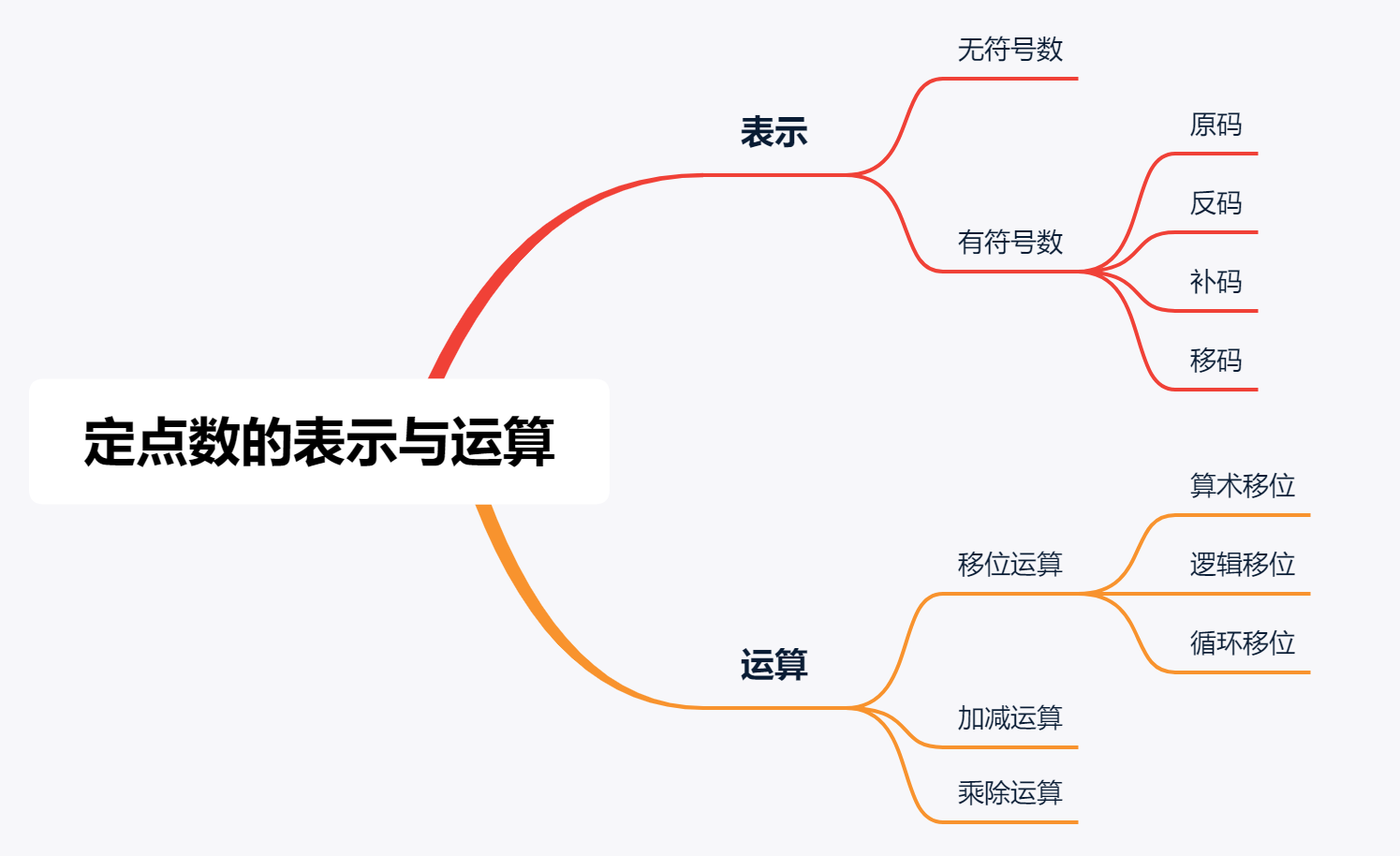
基础知识
真值和机器数
真值:正负号加上某进制数的绝对值的形式。+1101,-1011等。给人看的。
机器数:正负号采用数字表示的形式。一般采用0表示"+",1表示"-"。给机器看的,通常采用原码、补码、反码、移码表示。
BCD码
二进制编码的十进制数(Binary-Coded)通常采用4位二进制数来表示一位十进制数。常用的BCD码有8421码、余三码、2421码。
校验码
码距定义:任意两个合法码之间二进制位数不同的最小值。若最小仅有一位不同,码距就是1.
| 奇偶校验码 | 海明码 | 循环冗余校验码CRC |
|---|---|---|
| 能发现数据中奇数个位出错情况,无法发现偶数个位出错情况。不具有校验能力 | 能检测2位错误,并能纠正1位错误 | 可以检测所有奇数个位错误、所有双比特的错误,以及任何长度小于校验位长度的连续错误。 |
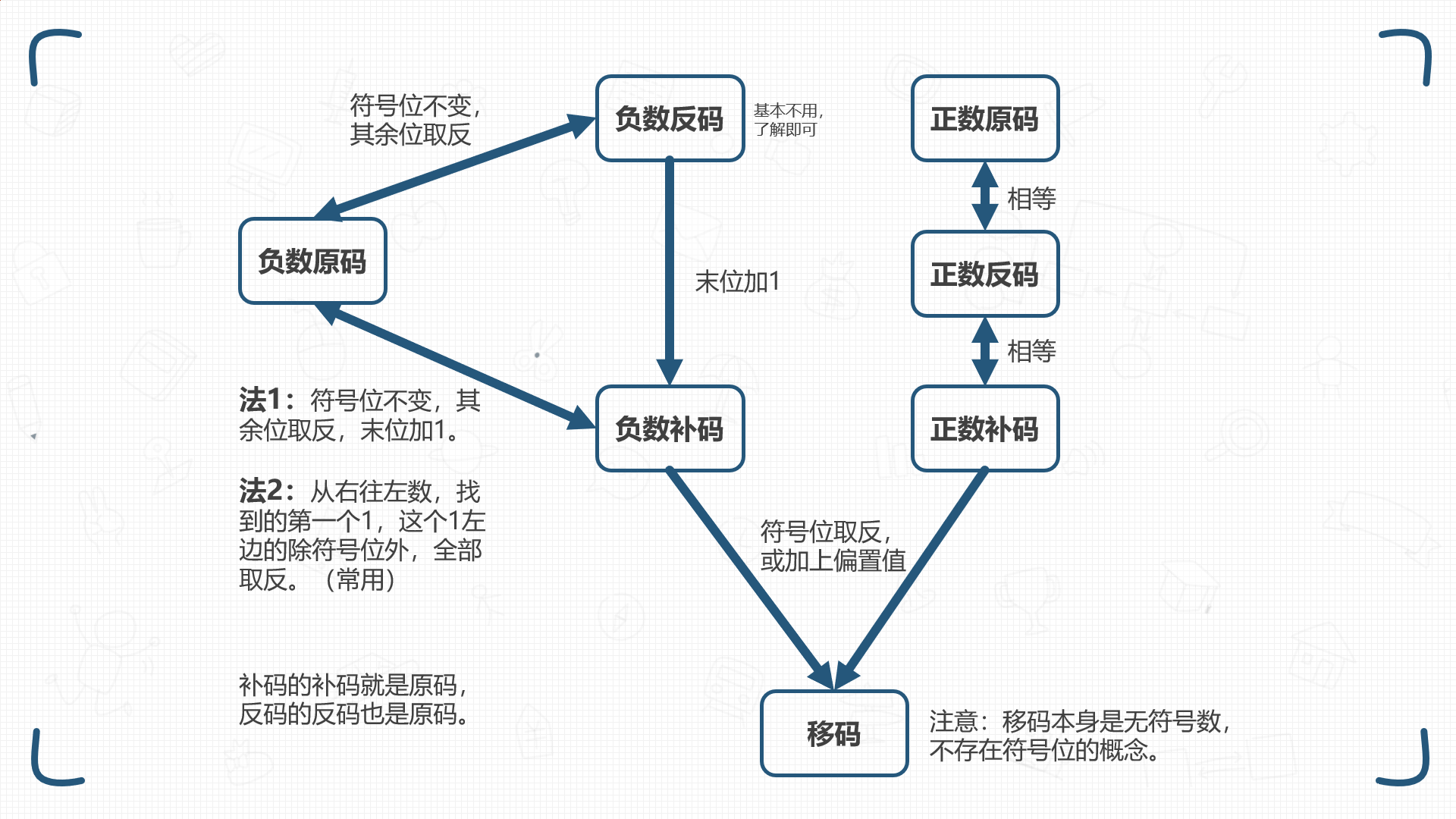
正数的原码,反码和补码
正数的原码最高位为符号位,用0表示。其余位为数值位。
正数的原码,反码,补码表示完全相等。
负数的原码,反码和补码
负数的原码最高位为符号位,用1表示。其余位为数值位。
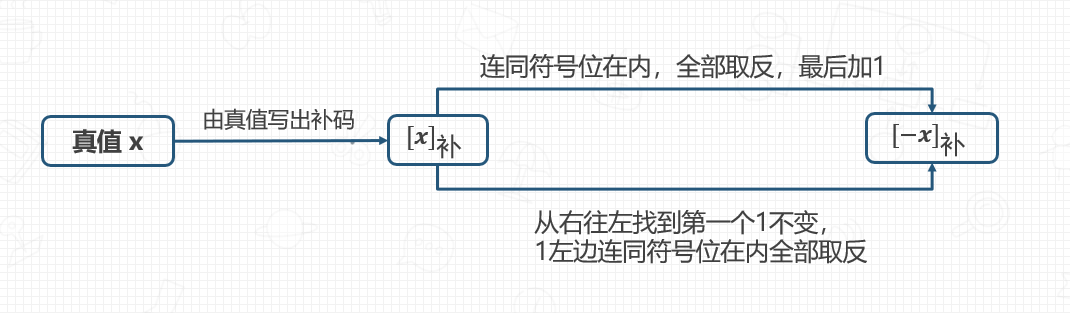
求补
对一个数x求补,就是求x相反数的补码$[-x]_补$。求补运算在汇编语言中用NEG表示。
变补
变补就是在原来符号位的基础上再增加一位来表示符号位,也就是两个符号位。变补又称为模4补码
x=-1010
补码:
10110 变补:110110
00:结果为正 11:结果为负
01:上溢 10:下溢
记忆:符号位最高位仍代表真正符号,0为正数,01代表上溢。1位负数,10代表下溢
模2加就是相加后模除以2(也就是除以2,取余数)
模4加就是相加后模除以4。也就是说模n,就是对最后结果取模n,对于二进制来说就是只保留最后n位。
移码
移码,也称为偏移值为M的移码表示。它允许我们使用无符号二进制来表示有符号整数。有点类似哈希映射的概念
个人理解:其实所有的编码原码,反码,补码和移码都可以看做无符号数。这些编码都是将有符号数映射的无符号数。只不过移码和原来真值之间的映射很直接,真值小,则映射的无符号数就小。真值大,映射的无符号数就大。这样便于计算机比较。计算机可不管符号是什么,他只会将两个二进制数相加。
将一个有符号整数x加上一个偏移值M,就得到一个非负整数,可以看作是无符号整数。这样一个无符号整数,在存储(无符号数不存在+0,-0问题),比较大小(浮点数比较阶码大小)等运算时比较方便。
移码可以由补码的符号位取反得到。但这只是形式上的规律,我们应该将移码看成无符号数。移码的本质就是用无符号二进制数表示有符号整数。
吐槽一下:感觉有些教材写的比较怪,你都把有符号数偏移到非负整数区间上了,怎么可能还有符号位这一概念。
如果还存在符号位,补码的符号位取反。正数变负数,负数变正数,更是让人迷惑不解。况且将负数整体偏移到正数区间,原来的位数根本不够表示。只有看成无符号数才行。
举个例子,机器字长8位,可以表示有符号整数[-128, 127],如果加上偏移值M = 128使用移码表示,则移码取值为[0, 255]。这个可以看出两点:1. 移码是非负整数。2. 机器字长8位全部参与编码,不存在符号位这一概念。
注意区分移码取值和真值的区别:
移码作为无符号数的值和真值之间就相差一个偏置值。这个比原码,反码和补码作为无符号数的值很真值之间的映射关系更为直接,简单。
假设偏移值M = 127,当移码值为10的时候,对应的真值就是10 - 127 = -117。而这个-117就是你原先想要存储的真值。
移码对应的真值范围和补码是一样的。假设机器字长$n + 1$。1位符号位,n位数值位。则补码和移码能表示的真值范围为$[-2^n, 2^n - 1]$。
也就是说移码将$[-2^n, 2^n - 1]$ 逐一映射到了$[0, 2^{n+1} - 1]$ 区间上。通常这个偏置值取最小负数的绝对值$2^n$。也就是将最小负数$[-2^n]_补$映射成$[0]_移$。同样真值0的移码表示也是唯一的,将$[0]_补$映射成$[2^n]_移$
原码、反码、补码表示范围
参考CSAPP 中负权值的概念,下面的表示范围会很好理解
假设机器字长为n+1:1位符号位,n位数值位。这里只列出前八位
| 定点小数编码 | 最大真值 | 最小真值 |
|---|---|---|
| 原码 | $1-2^{-n}$ | $-(1-2^{-n})$ |
| 反码 | $1-2^{-n}$ | $-(1-2^{-n})$ |
| 补码 | $1-2^{-n}$ | -1 |
| 定点整数编码 | 最大真值 | 最小真值 |
|---|---|---|
| 原码 | $2^n - 1$ | $-(2^n - 1)$ |
| 反码 | $2^n - 1$ | $-(2^n - 1)$ |
| 补码 | $(2^n - 1)$ | $-2^n$ |
原码0的表示有两种,+0和-0的表示是不一样的。而补码中0的表示是唯一的,所以补码比原码多表示一个数,也就是负数最小值。
假设机器字长为8位包括1位符号位,7位数值位。补码表示定点整数最小值是$-2^7 = -128$,那么-128的二进制补码形式是1000 0000。这个在原码中表示$-0$ 。这样理解也有点问题,可以参考下面的回答,从各个角度解释了补码。主要记者补码最小值的二进制形式,对解题有帮助。
https://www.zhihu.com/question/20159860
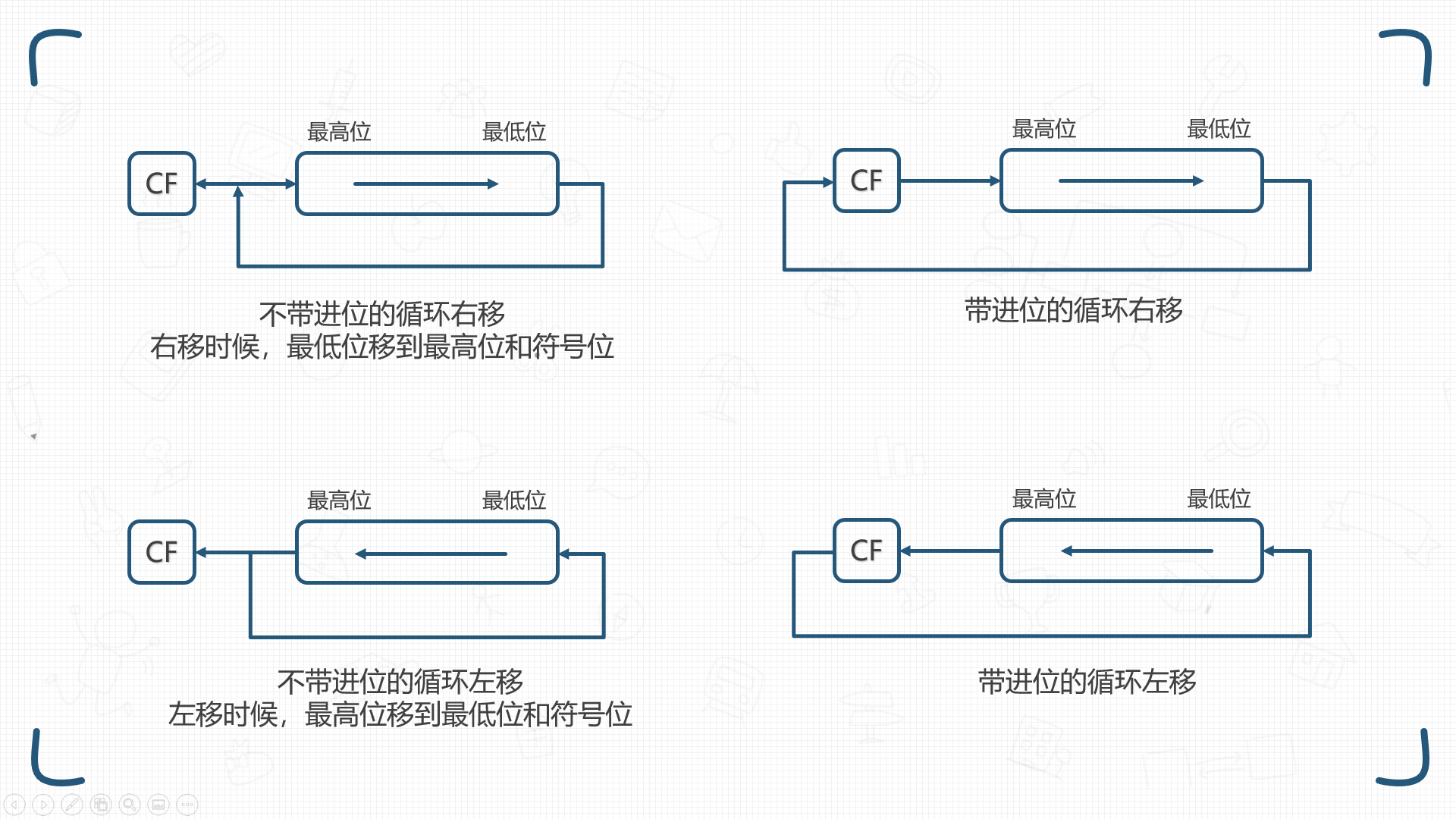
移位运算
算术移位的对象是有符号数,移位过程中符号位保持不变。
| 码制 | |
|---|---|
| 正数原码、反码、补码 | 0 |
| 负数原码 | 0 |
| 负数反码 | 1 |
| 负数补码 | 左移添0,右移添1 |
算术移位中比较重要的是负数补码。
逻辑移位将操作数数看做无符号数,不管是左移还是右移,都添0
浮点数的表示与运算
浮点数
计算机中可以这样表示数据:把一个数的有效数字和数的范围在计算机的存储单元中中分别予以表示。这种把数的范围和精度分别表示的方法相当于小数点的位置随比例因子的不同而在一定范围内可以自由浮动,所以称为浮点表示法。
通常,浮点数表示为 $$ N = r^E \times M $$ 可见浮点数由阶码和尾数两部分组成
- r是浮点数阶码的底,通常隐含,与尾数基数相同。
- E是阶码,反应浮点数的表示范围及小数点的位置
- M是尾数,M的位数反应浮点数的精度
规格化浮点数的尾数M的绝对值应满足条件:$\frac 1 r \leq |M| \leq 1$
| 编码 | 规格化形式 | 最大值形式 | 最小值形式 | 表示范围 |
|---|---|---|---|---|
| 原码正数 | 0.1xx...x | 0.11...1 | 0.10...0 | $\frac 1 2 \leq M \leq (1-2^{-n})$ |
| 原码负数 | 1.1xx...x | 1.10...0 | 1.11...1 | $(1-2^{-n}) \leq M \leq - \frac 1 2$ |
| 补码正数 | 0.1xx...x | 0.11...1 | 0.10...0 | $\frac 1 2 \leq M \leq (1-2^{-n})$ |
| 补码负数 | 1.0xx...x | 1.01...1 | 1.00...0 | $-1 \leq M \leq -(\frac 1 2 + 2^{-n})$ |
因为计算机一般以补码形式存储的,所以补码的规格化浮点数表示范围是重点。
在确定浮点数的表示范围时,根据浮点数的真值表达式可以发现,起决定作用的是E和M:M最小,E最小,则真值最小;M最大,E最大,则真值最大。
根据补码的表示范围,阶码很好确定。关键是规格化后尾数的补码有点不同,需要特别注意。
浮点数基数
两个规格化的浮点数,当长度相同时,基数越大所能表示数的个数越多。
对于基数为$2^k$的规格化浮点数,尾数用补码表示:正数的尾数最高k位不全为0;负数的尾数最高k位不全为1。
基数为2时,正数尾数最高位为1;负数最高位为0。
基数为4时,正数尾数最高两位不全为0;负数最高两位不全为1。
基数为8时,正数尾数最高三位不全为0;负数最高三位不全为1。
IEEE 754标准
IEEE 754标准规定常用的浮点数有:短浮点数(单精度,float)、长浮点数(双精度,double)。浮点数格式为
| S | E | M |
|---|---|---|
| 符号 | 阶码,用移码表示 | 尾数,用原码表示 |
| 类型 | 符号 | 阶码 | 尾数 | 总位数 | 阶码偏置值 |
|---|---|---|---|---|---|
| 短浮点数 | 1 | 8 | 23 | 32 | 127 |
| 长浮点数 | 1 | 11 | 52 | 64 | 1023 |
阶码的偏置值为127,空出来的8位全1表示无穷大。全0表示非规格化数。因此E的取值范围为[1, 254]
一个规格化的32位浮点数的真值可以表示为: $$ (-1)^S \times 1 . M \times 2^{E-127} $$
一个规格化的64位浮点数的真值可以表示为: $$ (-1)^S \times 1 . M \times 2^{E-1023} $$
可以发现,实际存储的时候只需要存储符号S、阶码E和尾数M。
特别注意是M代表是小数部分,整数部分1默认不存储的,这样可以多表示一位尾数,提高精度。 所以在IEEE 754标准转换十进制表示时,不要忘了尾数M的整数部分1。
特别地,阶码全0和阶码全1用作了特殊用途。则短浮点数阶码E的取值范围为$[1, 254]$,长浮点数阶码E取值范围为$[1, 1023]$。
| 阶码E | 尾数M | 含义 |
|---|---|---|
| 全0 | 全0 | 根据符号位,表示$\pm0$ |
| 全0 | 非0 | 没有隐藏位的非规格化数 |
| 全1 | 全0 | 根据符号位,表示$\pm \infty$ |
| 全1 | 非0 | NaN(Not a Number) |
下面是在二进制中常见的表示方式,应体会这样表达的思想。 $$ \begin{aligned} 1.1 &= 2 - 2^{-1} \ 1.11 &= 2 - 2^{-2} \ 1.111 &= 2 - 2^{-3} \ &... \ 1.1...1 & = 2 - 2^{-n} \end{aligned} $$
下面讨论一下IEEE 754浮点数的范围,只讨论正数的范围。因为负数只是在正数的基础上加负号:将正数最大值变成负数最小值,正数最小值变成负数最大值。
对照真值表达式,抛开符号S不谈,可以发现起决定作用的是M和E:M最小,E最小,则真值最小;M最大,E最大,则真值最大。应该学会推导。
| 格式 | E最小 | 1.M最小 | 代入真值表达式得最小 |
|---|---|---|---|
| 单精度 | 1 | 1.0 | $1.0 \times 2^{1-127} = 2^{-126}$ |
| 双精度 | 1 | 1.0 | $1.0 \times 2^{1-1023} = 2^{-1022}$ |
| 格式 | E最大 | 1.M最大 | 代入真值表达式得最大 |
|---|---|---|---|
| 单精度 | 254 | $1.1...1 = 2 - 2^{-23}$ | $(2 - 2^{-23}) \times 2^{254-127} = 2^{127} \times (2 - 2^{-23})$ |
| 双精度 | 2046 | $1.1...1 = 2 - 2^{-52}$ | $(2 - 2^{-23}) \times 2^{2046 - 1023} = 2^{1023} \times (2 - 2^{-52})$ |
为什么偏置值取127
浮点数在比较大小时候,先比较符号:符号不同直接判定大小;符号相同再比较阶码;阶码相同再比较尾数;这也是为什么符号位在最前,阶码其次,尾数再最后。
对于单精度浮点数,阶码8位采用补码表示,可以表示的真值范围为:$[-128, 127]$。但是补码不好比较大小,于是加上一个偏置值,统一转成非负整数,也就是无符号数表示。
本来应该加上128,也就是将$[-128, 127]$逐一映射到$[0, 255]$。但是255的8位二进制是1111 1111 规定表示无穷大。0对应的二进制0000 0000规定表示非规格化数。此时就只能将$[-126, 127]$映射到$[1,254]$上,此时偏置值为只能设为127。相当于少表示了两个负数,况且$2^{-128}$已经很小了,看成机器0,对精度影响不大。
所以,IEEE 754中所谓的阶码,本质上是一种移码,是无符号数,是有符号阶数的映射。需要减去偏移值才能得到原来的真值。
所有编码系统的设计,都在追求连续性和唯一性。
反码去掉间断点,提高连续性。补码在反码基础上,去掉重复点,保证唯一性。
定点数的加减乘除运算




 秋叶依剑
秋叶依剑